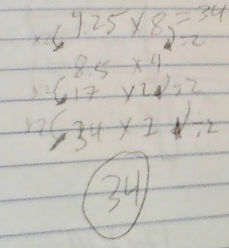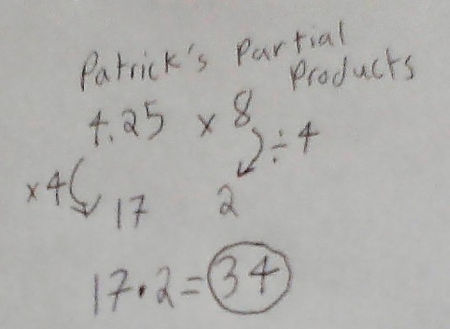How Can We Adapt Number Talks for Distance Learning? Insights from Richie Moreno

With Intro and Conclusion by Andrea Barraugh

As we move toward reopening schools, we all have many decisions to make about what is essential content and instruction in our math classes.  Number talks are an essential classroom practice and, with a few adaptations, can be facilitated in-person, online, and asynchronously.

What Is a Number Talk?

For those of you who are new to number talks, here are two ways you can learn about them:

1. Watch this video clip where Jo Boaler explains what a number talk is: Boaler Number Talk Explanation
2. Watch this video excerpt of a number talk in a fourth grade classroom:

This is a fourth grade in-person number talk.  Students share strategies, teacher records, and then students interact with the different strategies.

In a nutshell, number talks are a 10-15 minute math routine focused on mental math, number sense, procedural fluency, and math discourse.  There are many variations but the basic structure goes like this:  The teacher presents a math problem, students solve it mentally, discuss their strategies with a partner, and share their strategies publicly while the teacher listens, records their thinking, and facilitates student to student interaction.   When teachers and students engage regularly in number talks, they collaboratively build a classroom culture of curiosity, flexible thinking, making sense of numbers and operations, confidence-building, and risk-taking (Boaler, 2017; Parker & Humphries, 2015; Parrish, 2010). This environment can be built in an in-person or virtual classroom.

Number Talks with Distance Learning

After exploring a variety of ways to implement number talks effectively in the distance learning environment, our network of teachers made some discoveries we think are worth sharing.   In this post we will highlight an asynchronous adaptation from Richie Moreno and his sixth grade students at Innovation Middle School in San Diego, California.  Mr. Moreno and his students made a discovery that extends number talks into writing math explanations and interactive student feedback cycles.

Meet Richie Moreno and His Students

Richie Moreno is a sixth grade teacher at Innovation Middle School, a sixth – eighth grade STEAM-focused school in San Diego USD with a diverse population of approximately 500 students.  The ethnic breakdown of the student population is:  56 percent Hispanic, 22 percent white, 6 percent Asian, 5 percent African American, and 11 percent mixed race  or other. Seventy-one percent of the students fall into the category of socioeconomically disadvantaged and 15 percent are categorized as English Learners.  We worked with Mr. Moreno and his math team through the 2019-2020 school year during which time we focused on the implementation of number talks.  It is important to note that Mr. Moreno is a natural at creating a student-centered classroom with a culture of safety, inclusion, and valuing student voices.  He focused intensely throughout the year on integrating number talks into the classroom culture.

Mr. Moreno’s Asynchronous Adaptation
A Focus on Writing, Analysis, Feedback, and Interaction

I, like most teachers, was caught off-guard by Covid and distance learning. I knew from the start that I wanted to somehow continue our work with number talks, but I wasn’t sure how I could make it work in the new online environment.  I also wanted to make sure to include as many students as possible, knowing that a portion of my students may not attend synchronous sessions.

My students were comfortable with Google Forms, therefore I chose to use Forms as a vehicle for asynchronous number talks.  I decided to use an asynchronous format because, at the time, I was unfamiliar (and assumed students were, too) with video-meeting applications like Zoom.  My instinct was also that students would generally be apprehensive sharing-out in a video format and that the shy, quiet kids would be even more overshadowed by the more extroverted and talkative students in that setting than they would in the classroom.  It took me a few weeks of trial and error, but I eventually found a format and process that produced an asynchronous number talk experience that exceeded any prior expectations.  Of course, like everything, the format and process of this asynchronous number talk will continue to evolve and improve.  My hope is also that I can have input and suggestions from the math-educator/learner community.

The Process

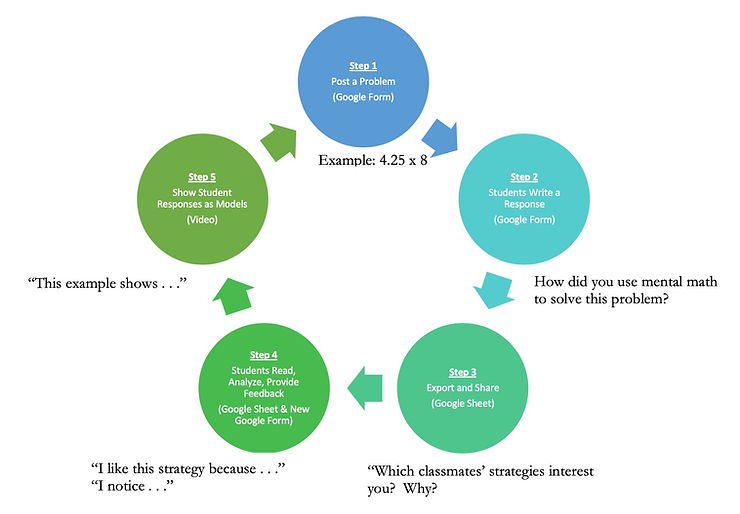
Step 1: Post the Problem

During distance learning, my students knew to check my Google Site daily.  Our asynchronous number talks spanned 2-3 days. On the first day, I posted a number talk problem on my Google Site.  I gave students instructions to use mental math to solve the problem with whatever strategy they chose.  I then asked them to fill-out a Google Form.

Step 2: Students Write a Response

On the Form, they entered what they thought the answer was, and then explained in words how they used mental math to solve the problem.  This is where the magic happened and why I’m so excited about sharing this model of  asynchronous number talks!  The byproduct of doing number talks this way is that students are forced to write about their thinking, an activity which supports sense-making in mathematics (Burns, 2004; NCTM, 2000; Zinsser, 1988).

The act of writing about one’s own math thinking is a metacognitive experience; students must confront their own processes, conceptions, and misconceptions.  Maybe even more importantly, the process of writing slows things down, which almost always allows for deeper thinking and an appreciation for noticing nuances and patterns in numbers.  William Zinsser captures this idea when he writes, “Writing organizes and clarifies our thoughts. Writing is how we think our way into a subject and make it our own. Writing enables us to find out what we know—and what we don’t know—about whatever we’re trying to learn.” Another benefit of having students put their thinking in writing is that it gives the teacher valuable information about how their students are thinking about numbers, including common misconceptions that can be addressed later.

I often find that many of my students, especially English Learners, are intimidated when I ask them to write.  They seem overly worried about grammar and spelling at the expense of the content of their ideas.  I find it helpful to de-emphasize spelling and let them know we are interested in their mathematical thinking.  This seems to lower their affective filters and elicit higher quality responses from all students.  My observations are validated in ideas put forth by Standford’s Understanding Language Project, “Instruction should focus on uncovering, hearing, and supporting students’ mathematical reasoning, not on accuracy in using language.”

Step 3: Export Responses to a Google Sheet & Share with Students

I set up the Google Form so student submissions would go to a Google Sheet.   During day one, as students were submitting responses, I would check the spreadsheet every hour-or-so, eager to see how my students were thinking about the problem.  I was thrilled that students who were normally quiet and reluctant to share their thinking in class were writing wonderful, insightful explanations.  Students were applying strategies that I hadn’t anticipated to solve the problem in simple, efficient ways.

Below are some samples of student strategies from an asynchronous number talk that I did back in early April.  The problem was:  4.25 x 8.

Student Sample A:  Doubling and Halving

Tawika (pseudonyms used to protect student identities) demonstrates understanding that if you double one factor and halve the other, the product stays the same.

Student Sample B: Multiplying One Factor by Four and Dividing by the Other Factor by Four

 

Patrick used a variation of “doubling and halving.”  His explanation shows an intuitive sense of inverse proportionality, as he multiplied one of the factors by four, and then to compensate, divided the other factor by four.  This created a more manageable multiplication problem for him.

 Student Sample C: Decomposition, Distribution, and Connecting to Money

 

Lyla used  money as a strategy for dealing with the 0.25. She thought of 0.25 as 25 cents.  She also used decomposition by friendly numbers and/or place value.

While the responses above all show students who successfully solved the problem with well-chosen strategies, I find as much or even more value in the responses that reveal student misconceptions. And better yet, these mistakes and misconceptions become a learning tool for other students.  There is so much value in misconceptions, and they deserve to be celebrated and appreciated as much as successes.  Neuroscience has taught us that people experience more brain growth when they work through disequilibrium versus when they arrive at the correct answer on the first attempt (Moser et al., 2011).

Student Sample D:  Partial Products and a Misconception

 

Mica appears to have a sense that she can decompose 4.25 into 4 and 0.25 but she only partially distributes the 8 and then uses division. 

Step 4: Students Respond to One Another’s Strategies

The day after students submitted their responses, I shared the Google Sheet (where all of the student responses are collected) with all of my students.  I had them fill out another Google Form, in which I prompted them to read other student responses, choose a strategy they were interested, and to explain why.  I also ask them to reflect on their own strategy and fix any errors they made.
The samples below come from a number talk in which students solved the problem 0.85 – 1/4 + 50%.   Previously we had explored the connections between fractions decimals and percents through experiences which were sometimes contextualized and sometimes contextualized.

Student Sample E

 

This student identifies “short” yet “detailed” as valuable characteristics of an effective response.  He also values the conversion of every term into decimals.

 Student Sample F

 

From looking at a classmate’s strategy, this student noticed that converting rational numbers into percentages might make them easier to work with.

One way that I was able to give feedback to students was to comment directly on their Number Talk response. It took time, but I would go through each of their responses and write a sentence or two.  I would also often write a question in the comment.  In the following day’s follow-up Form, I would ask them to answer any questions I asked in my comments.  In my debriefings,  I found that students enjoyed this direct, personalized feedback.  The comments were public to the whole class, and students were encouraged to read not just the comment I left for them, but other comments, too.  This turned out to be a good way to create asynchronous discourse.  Students appreciated that their efforts were appreciated and acknowledged.  We all want an audience; it validates what we do, and students are no different.

Step 5:  Use Student Responses as Models

My intuition tells me that using student responses as models is a powerful way to guide student learning.  Therefore, given the distance learning environment, I developed an asynchronous routine for analyzing students’ written explanations.  Integrating student input from the feedback form, I created videos which highlighted effective features of different written explanations. In a synchronous environment, I would facilitate a discussion but, given the distance learning environment, I felt the videos would give a greater number of students access.

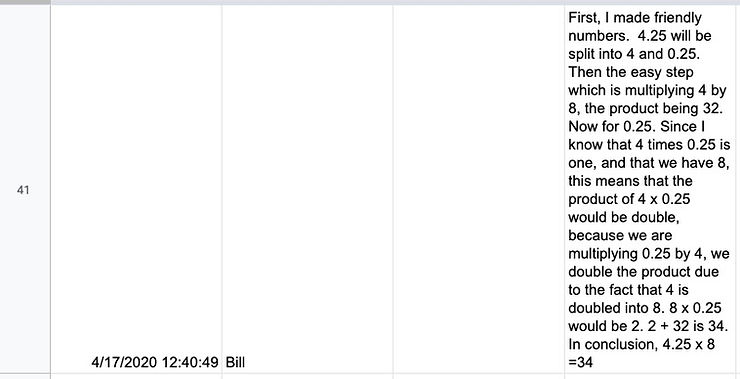
For the 4.25 x 8 number talk,  I used Bill’s response, displayed below.  In that video, I called attention to his use of sequential language, flow of logical thinking, and how having introductory clauses, such as “first, then, since, in conclusion,” really help the reader to follow the progression of his thinking.  

Next Steps 

My next step is to give students ways to show different strategies to solve the same problem.  In the Google Form, I am going to add a spot for students to explain other strategies they thought of to solve the problem, since we want students to explore multiple ways of doing the same problem.

Asynchronous number talks, regardless of whether distance learning happens next school year, will be a part of my classroom.  Based on the feedback I received, students enjoyed having access to the spreadsheet of responses to see how peers solved the problem.  Another big advantage of doing number talks asynchronously is that I get to hear from all of my students, something that does not happen during in-person number talks.  They provide a mechanism to elevate the culture of the classroom, where the students, not the teacher, lead the way. Please feel free to reach out to me if you have any ideas of how to improve this variation of number talks, or if you have any questions.

Concluding Thoughts

At Math Transformations, we read Mr. Moreno’s reflections with a sense of immense optimism for the future of students in his classroom and the classrooms of all teachers who embrace number talks as an essential feature of math instruction.  Mr. Moreno elevates student voices, is intrigued by their mathematical thinking, and goes out of his way to encourage students to harness the power of one another’s ideas. His perseverance during distance learning led to an effective adaptation of number talks that fits any classroom environment and integrates key elements of teaching and learning that we know are valuable.  An unintended outcome of his adaptation was that students’ math explanations on more complex tasks also improved.

References

Boaler, J. (2014).  How to Learn Math for Teachers and Parents: Number Talks.  Stanford Online Course. https://www.youtube.com/watch?v=yXNG6GKFhQM&feature=youtu.be
Burns, M. (2004). Writing in math. Educational Leadership, 62(2), 30-33.
Collins, A., Brown, J. S., & Newman, S. E. (1987). Cognitive apprenticeship: Teaching the craft of reading, writing and mathematics (Technical Report No. 403). BBN Laboratories, Cambridge, MA. Centre for the Study of Reading, University of Illinois. January, 1987.
Collins, A., Brown, J. S., & Newman, S. E. (1988). Cognitive apprenticeship.Thinking: The Journal of Philosophy for Children, 8(1), 2-10.
Moser, J. S., Schroder, H. S., Heeter, C., Moran, T. P., & Lee, Y. H. (2011). Mind Your Errors Evidence for a Neural Mechanism Linking Growth Mind-Set to Adaptive Posterror Adjustments.Psychological Science, 0956797611419520.
National Council for Teachers of Mathematics (2000). Principles and standards for school mathematics. Reston, VA. https://www.nctm.org/standards/
Parrish, S. (2010). Number Talks: Whole Number Computation. Math Solutions.
Parker, R. & Humphries, C. (2015). Making Number Talks Matter. Stenhouse.
Zinsser, W. (1989). Writing to learn: How to write – and think clearly – about any subject at all.   Harper and Rowe.