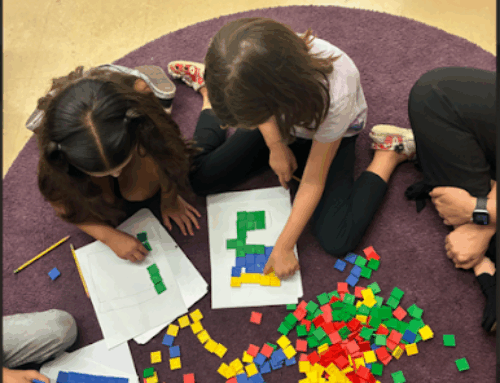For students to gain foundations for place value, the Common Core Content Standards call for kindergartners to compose and decompose numbers from 11 to 19 into ten ones and some further ones, using objects or drawings, and then record using equations like 18 = 10+8.
For some kindergartners this is a tall order, especially if these young students are still wrapping their brains around all the important counting ideas they need to conceptualize before tackling teen numbers. These counting concepts include:
One-to-one correspondence: Saying number words in correspondence with the objects counted.
Cardinality: Knowing that the last number word said when counting tells how many objects have been counted.
Hierarchical Inclusion: Knowing that each number represents one more than the previous number in a counting sequence and includes all previous numbers within it.
Number Conservation: Understanding that the quantity of a set doesn’t change if the set is re-arranged.
Number Sequence: Knowing the names and ordered list of number words
Subitizing: Visually recognizing the number of items in a small set without counting.
Unitizing is Not so Simple
Unitizing is a fancy word for a child’s ability to see numbers in groups, rather than always seeing numbers as individual units. So, for a child to look at the number 16 and really understand what it means, they should know that the ‘1’ is a group of ten, and the ‘6’ means six more ones. Learning to unitize is not easy, and to top it off, the way we read and say teen numbers in English can make things confusing.
Language Can Support or Confuse
The way we say teen numbers varies depending on the language we use. Some languages do a better job than others in supporting students’ understanding of the quantities these teen numbers represent.
For example, in Mandarin all the teen numbers follow a consistent pattern that supports the base ten number system. The number 11 in Mandarin literally means ten-one, the number 12 means ten-two, and the number 13 means ten-three, and so on up to 19, reinforcing the idea that these teen numbers stand for a group of ten and some extra ones.
This is in contrast with English, where the numbers 11-14 don’t follow the same pattern as the numbers 15-19. Eleven doesn’t provide the same support as the number sixteen. Spanish is like English in that the number trese (13) and catorse (14) don’t provide the same support as diez-y-seis (ten and six) or diez-y-siete (ten and seven).
Let the Students Guide the Teaching
Although the Common Core Standards state that kindergartners must be able to compose and decompose teen numbers, some children need more experience before they are ready to do so. The Standards are a good guide but listening and observing children is even better. When you notice that a child is still struggling with composing and decomposing numbers to 10, we recommend that they continue working on these smaller numbers until they build a solid foundation upon which to work with teen numbers.
Once students have built this firm foundation, there are some helpful tools and engaging activities to help them conceptualize teen numbers. Following are some of our favorites.
Using Ten Frames and Double Ten Frames
Fortunately, ten frames have become a staple in many primary grade classrooms. For those not familiar, a ten frame is a graphic tool that allows students to ‘see’ numbers and is an excellent way to help young children learn about teen numbers when they work with two ten frames at once. Here’s what a ten frame looks like:
This video explains how to use ten frames and provides some engaging activities to share with students. One of my favorite activities using ten frames is from Kathy Richardson’s book, Developing Number Concepts (Richardson, 1999). It’s called Two Ten Frame Addition. Check it out!
Using Number Paths
In Ann Carlyle’s book, It Makes Sense! Using Number Paths to Build Number Sense (Houghton Mifflin, 2020), she describes effective ways to use number paths to help children visualize numbers as being composed of groups and units.
On a number path, numbers are represented by rectangles, and each rectangle can be counted. Young children are much more comfortable with counting things, so a number path, which is a counting model, often makes more sense to them than a number line, which is a measurement
model. When working with a number path, students get valuable practice with one-to-one correspondence, number sequence, subitizing, cardinality, and seeing numbers in groups.
Number paths can also be used to introduce students to teen numbers. For example, Ann shows kindergartners an open number path without numbers and asks a series of questions:
“What do you notice?”
“How many blue squares are there? How do you know?”
“How many green squares are there? How do you know?”
“Where would we put the number 1? How do you know?”
“Where would we put the number 5? How do you know?”
“Where would we put the number 10? How do you know?”
“Where would we put the number 16? How do you know?”
As children conceptualize teen numbers, they begin to see these numbers as composed of a group of ten and some extras, and number paths can provide visual support. Number paths can also help transition students to working with number lines and Rekenrecks (Number Racks).
Using the Rekenreck
A Rekenrek, or number rack, is a rack that has two strings of ten beads each that are broken into two groups: five red beads and five white beads on top, and five red beads and five white beads on the bottom. It sort of reminds me of an abacus. This tool helps students ‘see’ that there are numbers within other numbers, and it helps children conceptualize teen numbers. Seeing numbers within other numbers can also be thought of as numbers ‘nested’ inside other numbers (5 is nested inside 6), which is another way to describe hierarchical inclusion, an important counting concept. In Jeff Frykhom’s Rekenreck Resource, he explains how to use this tool and shares many engaging activities. One of my favorites is called Flash Attack!
Here’s how it works. You quickly show students some beads on a Rekenrek, and the students’ job is to tell you how many beads they see. It’s like quick images, but with a Rekenrek. Following is an example of Flash Attack! showing students 17 beads:
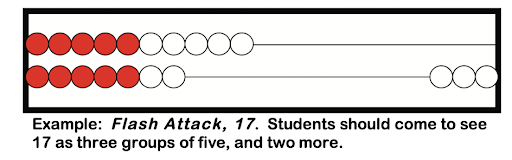
Flash Attack! helps students learn to think of one in broader ways. Frykholm explains that “Instead of one being limited to a single bead, students also come to think in terms of one group of 5 or one group of 10.”
Here’s an example of Flash Attack! showing students 13 beads:
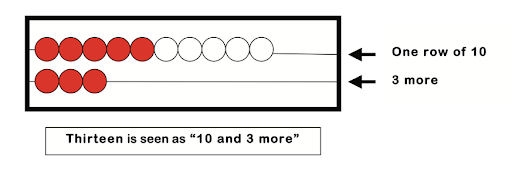
Using Number Games
The Investigations curriculum materials offer many engaging games that help students develop their number sense. In Roll and Record Teen Numbers, students compose and decompose teen numbers. Here’s how it works:
Partners use a deck of ‘teen number cards’. They turn over a card (e.g. 13), build the number using cubes, and figure out how to break it into two parts so that they have a ten and three extras. Then they record on a sheet like the one below.
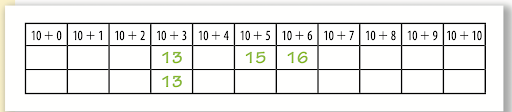
Race to 20
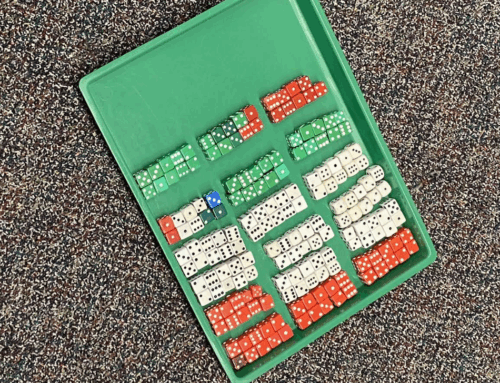
Race to 20 from Math Solutions, is an engaging game in which players roll a die and use counters to build that number on their double ten-frames. The player who reaches or goes over 20 first is the winner.
The game helps students “see” groups of numbers, engages them in counting to 20 and beyond, and gives them practice building teen numbers. Here’s a picture of two players’ double-ten frames after finishing a game:
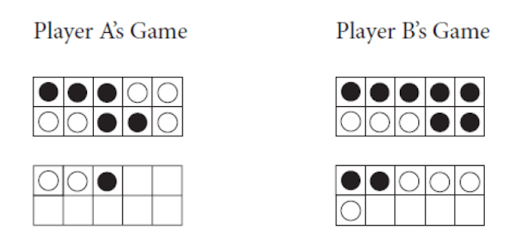
Building a Strong Foundation for Future Success
It’s not surprising that foundational number sense is a strong predictor of math achievement in elementary school (Jordan et al. 2009). And it’s through lots of experience with counting and decomposing numbers 1-10 that kindergartners build their number sense.
Once they have built a strong foundation with these smaller numbers and are ready to tackle numbers from 11-19, students will benefit from engaging activities that use helpful tools like ten frames, number paths, and rekenreks. We hope you’ll try out some of these recommendations with your students!