What Makes a Good Math Assessment Question?

Rusty Bresser
 There are many reasons why assessment is important to teaching and learning. Assessment gives us a window into our students’ mathematical thinking. It guides our instruction, helping us make decisions in the moment. We use assessment data to inform stakeholders about student and school progress. Assessment paves the way for productive feedback so that students can improve their learning. And if we invite our students into the assessment process, it can engage them in metacognition: the ability to think about and regulate their own thoughts.
There are many reasons why assessment is important to teaching and learning. Assessment gives us a window into our students’ mathematical thinking. It guides our instruction, helping us make decisions in the moment. We use assessment data to inform stakeholders about student and school progress. Assessment paves the way for productive feedback so that students can improve their learning. And if we invite our students into the assessment process, it can engage them in metacognition: the ability to think about and regulate their own thoughts.
Hopefully, we are moving away from asking our students a question, taking a few answers from the entire class, and then think that this is the same thing as learning (Fisher & Frey, 2007). Assessment is much more than taking a small sample and then extrapolating about what kids know and understand. Grant Wiggins amplifies the importance of assessment and its purpose when he says that, “the more you teach without finding out who understands the concepts and who doesn’t, the greater the likelihood that only already-proficient students will succeed.”
Assessing is like opening up a kid’s brain and taking a peek at what’s inside. Since we can’t literally do that, we need to find ways to get students to showcase what they know about whatever it is we are teaching them. And we need a good instrument to give us that information. Oftentimes, it’s the kinds of questions we ask that can either reveal a wide range of rich mathematical thinking from the students in our class, or not. So, what makes a good math assessment question?
Features of a Good Math Assessment Question
One of the features of a good math assessment question or problem is that it provides opportunities for students to demonstrate conceptual understanding, procedural fluency, and mathematical reasoning or problem solving (Stanford, 2018). Good assessment questions elicit explanations, diagrams, and justifications for an answer. A good assessment can yield responses that allow a teacher to analyze evidence of student learning that goes beyond what students did right or wrong. We want a math question or problem that is open-ended enough to give us the range of student thinking in the class and make it easy to establish and define evaluation criteria for student performance. Finally, good math assessment questions are often situated in interesting, real-world contexts that give meaning and purpose to mathematics.
One of my favorite books I use to tap students’ prior knowledge about volume is Counting on Frank by Rod Clement. The book is about a boy and his sunglass-wearing dog named Frank who challenge themselves by creating different measuring, counting, and estimating scenarios. When they try to figure out how many ‘Franks’ would fit in the boy’s bedroom, I stop reading and ask students to think about how many ‘Franks’ would fit in their school classroom (or, if they are sheltering in place, in their own bedroom).
The question is a messy one that requires students to make sense of the problem and look for entry points that will lead to a solution pathway. I give them little direction because I am curious about many things. What do students already know about the concept of volume? What procedures will they use when figuring the answer? What problem solving strategies and math reasoning do they bring to the task? What do they know about length, width, height? What do they use as a ‘Frank unit’ of measurement? Are their estimates reasonable? Do they already have an intuitive knowledge of the formula for finding the volume of a rectangular prism? Can they access measuring tools, and do they know how to use them? How do they work with others?
Open-ended assessment questions cast a wide net and can give us answers to questions like the ones above that traditional, closed-ended questions cannot. The book Counting on Frank is full of situations that can lead to engaging math questions. And the How many Franks problem is a nice way to launch a unit on volume. Another good math assessment question from Illustrative Math (2016) is called Cari’s Aquarium.
Cari’s Aquarium
The Cari’s Aquarium, from Illustrative Mathematics, is another example of an open-ended assessment that is challenging yet can reveal so much about students’ thinking regarding volume. Here’s the question:
Cari is the lead architect for the city’s new aquarium. All the tanks in the aquarium will be rectangular prisms where the side lengths are whole numbers…Cari knows that a certain species of fish needs at least 240 cubic feet of water in its tank. Create different rectangular prisms that would hold exactly 240 cubic feet. Which dimensions would be most appropriate for a fish tank? Why?
I like this assessment question for many reasons. First of all, students are challenged to think about the dimensions of an aquarium that holds exactly 240 cubic feet, and to do this, they must apply what they know about volume. Not only do they have to create an aquarium that holds 240 cubic feet, but they also have to make as many different aquariums that they can think of that hold this amount of water. There are, in fact, many different possible answers, and this can lead students to the challenge of figuring out how many possibilities there are and how they might go about proving they’ve found them all.
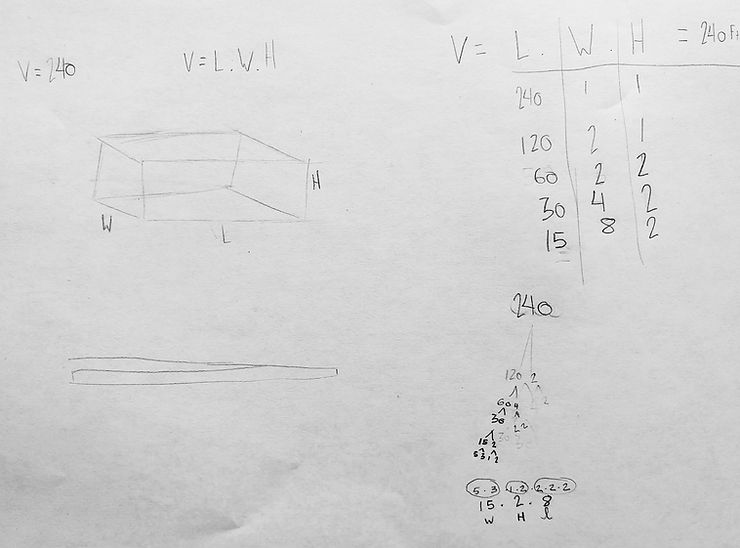
Student Response A: This student’s chart shows the different ways they found to create some of the aquariums. The chart is organized in such a way as to reveal some interesting patterns. Feedback might prompt the student to give a written explanation that might provide more insight into their thinking.
This assessment question provides students with the opportunity to showcase their understanding of the concept of volume, requires them to use procedures to figure out the answer, and it also engages them in problem solving and math reasoning. Furthermore, the problem is embedded in a real-world context that gives meaning to using mathematics, and this is where the last part of the question gets interesting. Once students create different possible aquariums, they must come up with an argument for which one(s) are most appropriate for a real-life aquarium (a 1 ft.-by-1ft.-by 240 ft. aquarium wouldn’t be very realistic!).
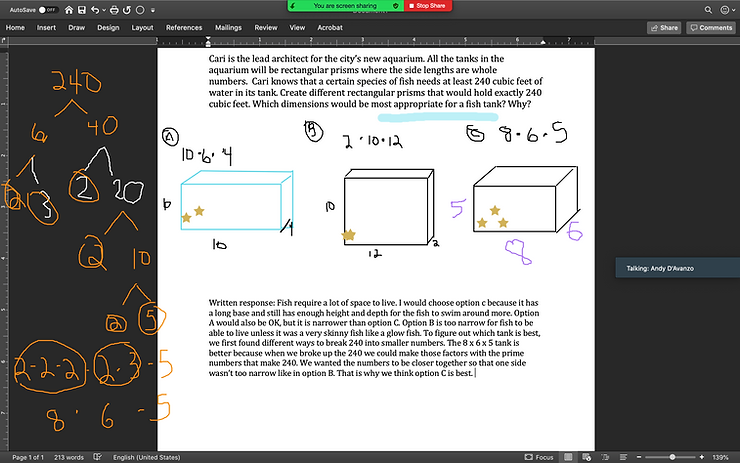
Student Response B: This is a collaborative effort by some students in a breakout room on Zoom. The students used a shared screen and animation, showing their work with factors, making diagrams of the various tanks, and providing a detailed argument as to why some of the aquariums are better for the fish than others.
In the NCTM publication, Teaching Children Mathematics (Vol. 21, No. 6, teaching children mathematics, February 2015) there is a fascinating discussion of this problem and how it offers students the opportunity to ‘decontextualize’ (find the dimensions of all the possible aquariums and represent them symbolically), and to ‘contextualize’ (to think about what the numbers mean and what they represent given the aquarium context). Cari’s Aquarium allows us to see how students reason abstractly and quantitatively, construct viable arguments, and look for and make use of patterns, all important activities we want students to engage in.
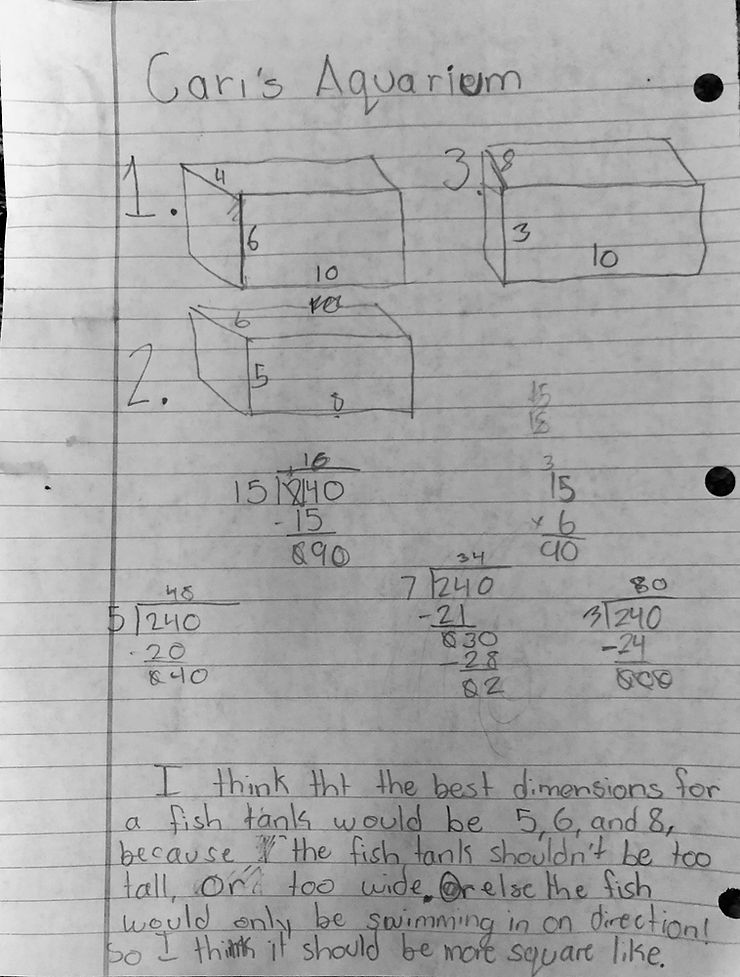
Student Response C: This student clearly shows how they arrived at some different aquarium possibilities using division. Their written explanation reveals their conjecture that the tank “should be more square- like,” not too tall or wide.
Assessment for Learning
In our current high-stakes testing environment, I often worry about the instructional time we lose when we spend so much time on testing. But if we focus our efforts more on what Joyner & Muri call ‘informative assessment’, and what Dylan William calls, ‘assessment for learning,’ then our perception can shift. When we ask good assessment questions, we are at once engaging students in worthwhile tasks that give us a window into their mathematical thinking. Once we see what students know and what they struggle with, we can provide productive feedback in order to accomplish the main goal of assessment: to improve student learning.