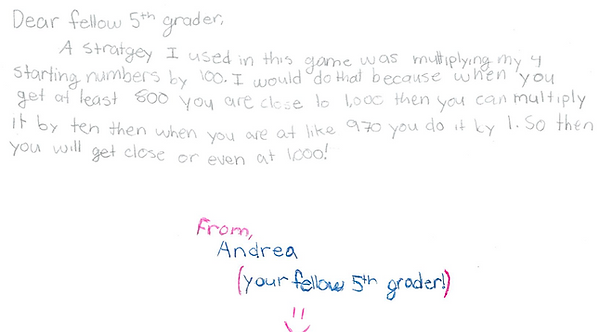Teaching Math for Understanding During Covid-19

Rusty Bresser
Since the pandemic began, there have been many challenges facing teachers, students, administrators, and families who are all trying to figure out how to manage in virtual environments. The pandemic has revealed limitations and exposed inequities in our educational systems. On the other hand, it has also shown how creative and responsive we can be when we are put to the test. And put to the test we have been. Even before covid-19 happened, teachers and administrators’ plates were full.
One challenge we face during the pandemic is to continue teaching mathematics in a way that focuses on meaning making. In recent years, with guidance from Common Core, teachers have begun to shift away from teaching that emphasizes rote memorization and move toward engaging students in rich tasks that help them develop mathematical understanding. We want to keep this momentum going through distance learning. But how? This post will explore what it means to understand a math concept, show examples of what understanding looks like, and share tips from local teachers who have experienced success teaching math for understanding in virtual environments.
What Does it Mean to Understand a Math Concept?
“Any fool can know, the point is to understand.” But what does it mean to understand something, especially when it comes to mathematics? David Perkins, in his article, Teaching for Understanding (Perkins, 1993) distinguishes between knowing something and understanding something. He says that a student might be able to regurgitate reams of facts and demonstrate routine skills with very little understanding.
Perkins describes understanding as being able to ‘perform’ different activities. Take the concept of multiplication for example. A student understands the concept of multiplication when they can:
These ‘performances’ show different ways that students understand the idea of multiplication. Yes, being able to recite the answer to 7×6 is important, but it doesn’t necessarily mean that a student understands the concept. If asked to explain how to solve 7×6 when they haven’t memorized it yet, and they respond by saying, “I know seven times six is forty-two because seven times five is thirty-five, and if I add one more seven, it’s forty-two,” then they have given you some evidence of conceptual understanding.
The Common Core Standards for Mathematical Practice identify similar activities that mathematically proficient students can perform. These activities include making sense of problems, abstracting situations and representing them symbolically, constructing arguments, modeling with mathematics, looking for and identifying patterns, applying concepts, using tools to solve problems, and using academic language precisely
What Does Understanding Look Like?
Understanding reveals itself in different ways. In a letter to a peer, this fifth grader explains her strategy for winning the game of Close to 1,000. In the game, a player rolls a die 7 times, each time making a decision whether to multiply the number on the die by 1, 10, or 100. As the player moves through the game, they add together the seven products in order to get closest to a score of 1,000.
This fourth-grade student was asked to figure out how many days she’s been alive. She provides evidence of how she made sense of and solved the problem step-by-step:
Although this second grader created a final equation that is not written correctly (29+10 = 39 + 2 =41), she does showcase her understanding of the concept of place value (“I know there is a ten in 12”).
This student reveals their understanding by writing a story context for the problem, -3 + 4:
“In the desert, it was -3 degrees Fahrenheit. Toward the morning, the temperature rose 4 degrees. What was the temperature?”
In the above examples, students were able to explain a winning strategy in detail, provide evidence of their thinking in solving a problem, show they understand the value of the digits in a number, and construct a context that gives meaning to the numbers and operation in a problem.
How Can We Facilitate Understanding While Teaching Virtually?
The Math Transformations website is a treasure trove of ideas and resources for distance learning. These resources can be life savers for teachers and students as they shift to online instruction. But what do teachers in the field have to say about what’s been most successful for them when teaching synchronously and asynchronously? In our work with local teachers, we have been hearing about their successes when teaching math for understanding in virtual environments. Following are some of their tips, suggestions, and favorite resources. Their ideas align well with the recent post-school closure recommendations put forth by the Council for Great City Schools.
Tip #1
Create a safe environment for virtual learning
Lowering the affective filter is key for any type of learning, but especially in virtual environments. Technology can create barriers for both the teacher and the student, so it’s vital that before posing cognitively challenging problems for students to solve online, we allow them time to navigate and learn to use online tools. Once they are comfortable with the technology, it’s also important that we give students time to just chat, ask questions, and share what’s going on in their lives. When they are comfortable communicating about everyday things, then we can ease them into thinking and communicating about mathematics.
Tip #2
Work with small groups when teaching synchronously
Teaching synchronously to a large group of students is very challenging. Teachers report that the best results happen when teaching math to a small group of students. The teacher and the students can ‘see’ everyone, there is more time for discussion and differentiation, and it is easier for teachers to assess understanding.
Tip #3
Allow for longer wait/think time When teaching synchronously, teachers have noticed that students need more time to process questions than they would in a face-to-face environment. Increase your wait time, and more learning and conversation is sure to happen.
Tip #4
Less is more
Even before online teaching and learning, we saw the value of posing fewer problems or teaching fewer lessons in order to give students more time to think, reason, and make sense. This is even more important in virtual environments, especially when teaching synchronously. Teachers have found that they are sometimes cutting the length of their lessons in half in order to keep students engaged and focused.
Tip #5
Make use of resources students have at home
While not all families have equal access to learning materials at home, there are some things most families do have that can support learning math with understanding. Recently, one of our student teachers taught a series of lessons online about capacity to her third graders. She had her students get a measuring cup and asked them what they noticed and what they wondered about the measuring tool. Then she had them use the measuring cup to estimate and then find out how many milliliters of water different containers in their kitchen would hold. This successful and engaging exploration is just one example of how to use everyday materials at home to support meaning making.
Tip #6
Make connections between asynchronous and synchronous teaching
One teacher reported that her grade level team used Zoom to synchronously introduce an open-ended math problem. The classes co-created expectations together before moving to Google Classroom where students worked asynchronously on the problem. Teachers used Google Slides in Google Classroom to provide individual feedback to their students before shifting back the next day to a Zoom meeting to discuss solution strategies. During the meeting, teachers found the chat box on Zoom useful, especially for those students who may be reluctant to share out in front of their peers.
Tip #7
Use online platforms that make it easier for students to communicate their thinking
Seesaw
Using Seesaw, teachers can videotape themselves giving instructions for math games or lessons so that their students can ‘see’ a familiar face rather than just reading directions. Students can communicate their mathematical ideas using video as well. All they have to do is press record and talk without having to write anything down.
Tip #8
Use online resources that make math visual
Illustrative Math Talking Math (math talks with photos)
Each “day” of this resource shows a photo and has a question for students to respond to for each grade level, K-5. Students are asked to think, notice, wonder, reason, calculate, and tap into their prior experience. All the teacher has to do is show the photo and make sure to ask students to explain their reasoning.
Tip #9
Use online resources that encourage students to think outside the box
Which One Doesn’t Belong?
This resource really pushes students to make sense of number, data, and shape and there are problems for all ages and grades. A typical picture shows four different numbers, shapes, equations, or photos, and students have to think about which one doesn’t belong and why. Which One Doesn’t Belong offers students opportunities to think creatively and make sense of mathematics in unique ways.
Tip #10
Use online resources that help students make real-world connections
Math At Home
This valuable Pre-K-5 resource is perfect for distance learning, both synchronous and asynchronous. The questions and problems focus on a multitude of math concepts and help students make real world connections, visualize, and communicate their math thinking.
Tip #11
Use virtual manipulatives
Virtual Manipulatives from Didax
Although having the real, three-dimensional manipulatives in hand is optimal for learning, virtual manipulatives can be an effective learning tool when solving math problems and representing mathematical thinking. One advice that teachers have about virtual manipulatives is to allow students time to explore these tools before using them in a math lesson.
Tip #12
Use online resources that require students to explain their reasoning
Splat Math
The problems in Splat Math can be used as number talks. Each slide shows an engaging and accessible visual that poses a math question. For young children, a slide might show a picture of 8 counters. Students are asked, “How many do you see?” Then, some of the counters are covered over by a ‘splat’ that looks like spilt milk. Students are then asked, “How many are covered up? How do you know? The problems engage students in sense making and discussion. There are Splat slideshows for grades K-8.
Tip #13
Use online resources that have math games for students to play
The link below from the Math Transformations website provides a list of math games with instructions for kindergarten. You will find links like this one on the website for every grade level. Teachers have found it helpful to videotape themselves modeling how to play the math games. Online platforms such as Seesaw make it easy to videotape and then share with students. Teachers report that using breakout rooms on platforms such as Zoom increase student engagement. As the host, teachers can visit the rooms to observe, provide feedback, and assess student learning.
Preparing the Way for the Upcoming School Year
Whether your school district will return face-to-face, online, or a combination of the two, things will be different, and teachers will benefit from being prepared for what’s to come. Hopefully, we can use what we’ve learned from our experiences and those of our colleagues to make online teaching meaningful for our students. Using strategies and resources that offer students opportunities to explain, muster evidence, make generalizations, apply what they’ve learned, use examples and analogies, and represent their thinking in new ways will help us keep our focus on teaching math for understanding.
What ideas do you have for teaching math for understanding in virtual environments?