3 Ways to Differentiate Math Instruction

Rusty Bresser
I used to think that I was meeting students’ needs by putting them in different groups during math class. The “high” students would be in one group. They got to do the problem-solving tasks because I mistakenly thought that only they were ready to tackle problems that required higher order thinking. The kids in the middle had their math work to do at their level (at least what I perceived as their level), and the resource kids were pulled out to work with the resource teacher. It was like a three-ring circus. For more info about the unintended impact of grouping practices and “high, middle, low” labels, listen to this clip from Jo Boaler.
Now I think about differentiating instruction differently. If we want all of our students to have access to the core curriculum, while also meeting their individual needs, we can do this by creating multiple paths to learning by asking open-ended questions, providing choice, and allowing students to showcase their learning in different ways.
Ask Open-Ended Questions
One of the easiest ways to differentiate instruction is to ask questions that elicit multiple perspectives. Open-ended questions may have more than one correct answer, can be solved in different ways and on different levels, and offer students room for their own decision making.
Here are some examples across the grades:
- I am a coin with a building on me. What might I be?
- You see a sign in a shop window that reads ½ off sale. What does this mean to you?
- I am thinking of some decimal numbers between 1 and 2. What might they be?
- How many numbers can you make with the digits 1,2,3,4? You can only use each digit once in each number.
- I have 6 eggs. Some are plain and some are fancy. How many of each could I have?
- I have 25 cents. What coins might I have? Show all the different possibilities that you can.
- Could $1 million actually fit into a standard-size briefcase? Assume the largest denomination in circulation is $100.
- I multiplied two numbers and got a product smaller than both numbers. What numbers might I have multiplied?
- A four-digit number was multiplied by a six-digit number to get a number close to two. What might these numbers have been?
- How many different ways can you show 2/3?
- Make up some different ways to add 9 to 23 in your head. In how many ways can you do it?
- The answer is 20. What might the question be?
Posing an open question elicits varied student responses and allows students to tackle mathematics with curiosity, entering the mathematics where they choose to start and taking it as far as they want to go. The examples below are from a second grade class where the teacher has high expectations for all students.
The answer is 57. What is the question?
In the samples below, Michael found structure in his exploration of the question, identifying a pattern and persisting from 58-1 = 57 to 59 – 2 = 57 all the way to 97 – 40 = 57.

Yen approached the question differently than Michael, beginning with trial and error and then finding a pattern. Once she found a pattern and a system, she applied it persistently. Can you figure out what she discovered?

What do you notice about Raul’s work? What system did he use? What did he discover?

These open-ended questions cast a wide net and can engage children who are at various skill levels and who might think about things in different ways. Some great resources for open-ended questions are the following: Good Questions for Math Teaching, K-5 by Peter Sullivan & Pat Lilburn; Good Questions for Math Teaching, 5-8 by Lanie Schuster & Nancy Anderson; and Good Questions for Math Teaching, High School by Nancy Anderson, et. al.
Offer Students Choices
My friend and colleague Susan Scharton posed the following story problem for a group of first graders to solve. Notice in the work sample below how Susan offered her first graders some choices. They could pick from four different number pairs, depending on their skill and comfort level. What’s important is that while students have choices, they all gain experience with the same problem type.
In the following sample, Kai not only got to choose which number pair she wanted to work with, but she also got to choose how she wanted to approach and solve the problem.

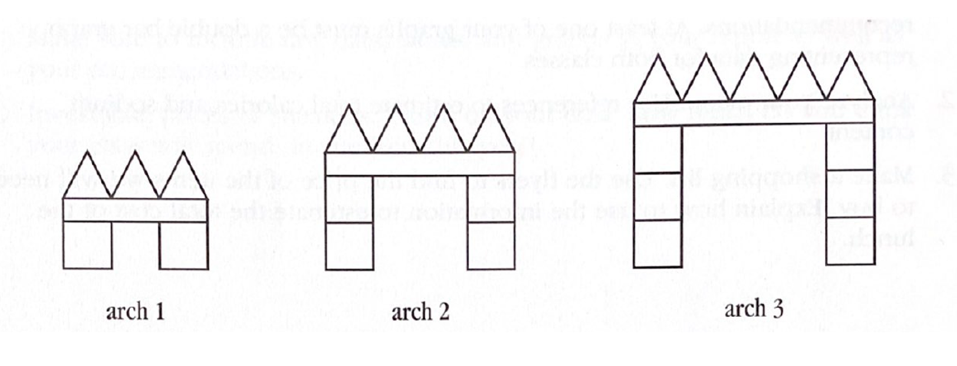
We can pose the same problem to all of our students, as long as we offer questions or choices that meet students at their skill level. The Arch Patterns is an example of a low floor, high ceiling problem from Linda Dacey and Jayne Bamford’s book, Math for All: Differentiating Instruction (2007) – Grades 6-8, Grades 3-5, and Grades K-2.
When I use this problem in math class, I start by showing the students a picture of the following arch pattern and asking everyone:
What do you notice? What stays the same? What changes?
Next, students choose from a variety of questions about the arch pattern. The questions vary in difficulty, and some require students to generalize about the pattern. The key is that students get to choose which questions to explore depending on their comfort and skill level. And everyone gets experience making predictions and thinking about how the arches change and how they stay the same. When the class comes together to discuss their thinking, all students benefit from the cross pollination of ideas.
Arch Pattern Questions
- How many pieces does it take to make arch 5?
- Draw arch 5.
- How many squares are there in arch 6?
- How many triangles are there in arch 7?
- How many pieces does it take to make arch 10? Explain your reasoning.
- How many pieces will it take to build arch 10? Explain your reasoning.
- In general, how can you use the arch number to find the number of triangles?
- How many pieces will it take to build arch 40? Show your work.
- How many pieces will it take to build arch 30? Explain your reasoning.
- In general, how can you use the arch number to find the number of squares?
- Rose Marie used 48 pieces to make an arch. What arch number did she make?
Allow for a Variety of Ways to Showcase Learning
We can meet students’ individual learning needs by letting them decide how they want to demonstrate their learning. This can be motivating, engaging, and fun for children. For example, sixth grade teacher Andy Jensen has his students show what they’ve learned using video on Flipgrid. Learning becomes a performance and a preferred way for some students to shine. Others like to draw diagrams or pictures, build models, show equations, or write about their thinking.
Provide Multiple Paths to Learning and Presume Competence
King-Shaver and Hunter (2003) remind us that at the core of true differentiated instruction is the creation of multiple paths to learning so that students have equal access to the course curriculum. Three of these pathways include asking open-ended questions, offering choices, and allowing students to demonstrate their learning in different ways.
When we think about differentiation and meeting students’ needs, the most important thing I think we can do as teachers is to presume that all of our students are competent at math. Believing in our students has a profound effect on their motivation to learn and is at the heart of differentiation.